
تُعتبر الرياضيات من المواد المُعقّدة بالنسبة إلى الكثير من الطُلاب.. إذ تشمل العِلاقات والقوانين والمُتغيرات التي تبدو مُعقد للوهلة الأولى، إلا أنه سُرعان ما تعتاد عليها، عند التركيز فيها والتعرف على وسائل حلّها، وقد تكون الدوال أصعبها؛ إذ تشتمل على العديد من الأنواع والرسومات البيانية.
العناصر
- مقدمة البحث.
- ماهية الدالة..
- ما هي أنواع الدالة؟
- تغيرات الدالة
- ما الفائدة من دراسة الدوال؟
- خاتمة البحث.
مقدمة بحث عن الدوال
بدأ انتشار مُصطلح الدوال في عام 1649 بعد اكتشاف العالم “غوتفريد لايبنتس” المُنحنيات والرسوم البيانية،
ثُم استخدم بعدها في مُنتصف القرن الثامن عشر من أجل التعبير عن الوسائط والصيغ الرياضية المُختلف.. فتوصل العُلماء إلى عدة قوانين وعلاقات تربط بين المُتغيرات من أجل الوصول إلى نتائج.
ماهية الدالة..
- إن الدالة المُثلثية إحدى العلاقات الرياضية التي تتكون من مُدخلات، ويلزم توافر المُدخلات من أجل الحصول على المُخرجات.
- تربط الدالة بين مجموعتين “المجال”، والذي يتكون من مجموعة من الأرقام، كُل منهم مُنفصل عن الآخر، والمجموعة الثانية تُعرف بـ “المجال المُقابل” أو “المدى”.
- يرتبط كُل عنصر أو رقم من المجال الأول برقم من المجال المُقابل، ويُعرف بـ “العنصر المُنفصل”.
- لا يُمكن ارتباط عُنصر من المجال بأكثر من عُنصر في المدى.
- يُعرف “المدى” بأنه مجموعة من القيّم “الأرقام” الفعلية الصحيحة للدالة.
- قد يكون المدى جُزءًا من المجال؛ وذلك في حالة عدم تغطية الدالة كافة قيم المجال.
لا يفوتك أيضًا: الميل كم كيلو متر يساوي
ما هي أنواع الدالة؟
تتعدد أنواع الدوال وتمتاز كُل منها بخصائص وقواعد مُغايرة عن الأخرى.
1- الدالة الثابتة
- قيمة التابع ثابت.
- لا يؤثر الوسط على قيمة التابع.
- تُرسم على هيئة خط مُستقيم يوازي محور “X” على الرسم البياني، ويُقاطع المحور “Y” في نُقطة.
- الصيغة الرياضية: f (x)= a
2- الدالة المحايدة
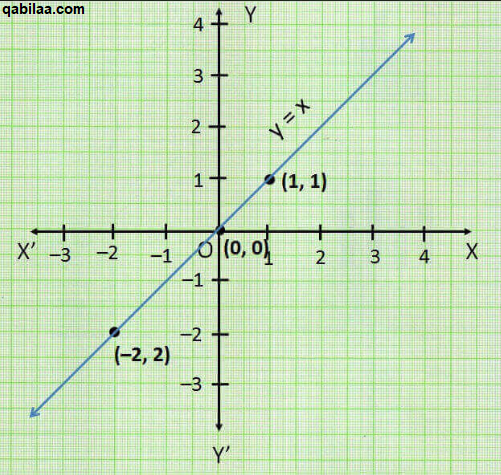
- تُعرف بالدالة المُتطابقة.
- ترتبط عناصر المجال بنفسها؛ حيث يكون المجال المُقابل مُطابقًا للمجال.
- تُمثل بيانيًا على هيئة خط مُستقيم مائل يقطع نُقطة الصفر.
- الصيغة الرياضية: f (x) = x
3- الدالة الجبرية
- يُطلق على الدوال التي تتطلب إجراء واحدة أو أكثر من العمليات الحسابية دالة جبرية.
- تضُم الدالة عددًا من الدوال الأخرى: “الدوال الابتدائية، دوال كثيرة الحدود، دالة القياس، دالة الصحيح، الدالة النسبية، دالة الجذر التربيعي”
- الصيغة الرياضية: f(x)=x² + 3x + 6
4- الدالة متعددة الحدود
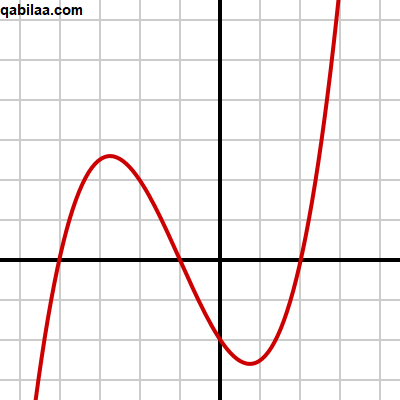
- يطُلق عليها الكثير من المُسميات: “كثيرة الحدود، الحدانية، ذات الحدود”.
- تتكون الدالة من مُعامل أو أكثر.
- قد تضّم الدالة عددًا من المتغيرات.
- يُمكن أن تكون الدالة من الدرجة “الأولى أو الثانية أو الثالثة أو الرابعة ….”.
- الصيغة الرياضية: P(x)=am(x)n + an – 1xn –1 + ⋯ + a1x + a0
5- الدالة التربيعية
- يُطلق عليها دالة كثيرة الحدود من الدرجة الثانية أو كثيرة الحدود التربيعي.
- تتكون من عددًا من المُعاملات، والتي يُمكنها أن تكون أعدادًا حقيقة أو غيرها.
- قد تشتمل الدالة على مُتغير واحد أو عدة مُتغيرات.
- الصيغة الرياضية: f (x) = ax2 + bx + c
- الدالة التربيعية أحادية المتغيرات: f (x, y) + ax² + by² + c(x * y) + dx + e(y) +f
- الدالة التربيعية ذات المُتغيرات الثلاثية: f (x, y, z) = ax² + by² + cz² + dxy² + e(x * z) + f (y * z) + g(x) I * z+ j +
لا يفوتك أيضًا: حساب الكوب كم مل
6- الدالة الكسرية
- يتم كتابتها على هيئة نسبة.
- تتمثل النسبة في “القيمة بين دالتين مُتعددي الحدود”.
- الصيغة الرياضية: R (x)= P (x) / Q (x)
7- الدالة المثلثية
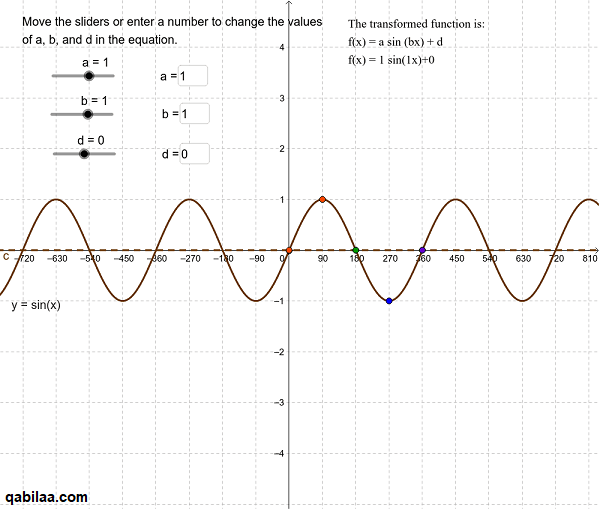
- تتوقف الدالة على العمليات الحسابية المُختصة بـ “حساب المُثلثات”.
- يتم رسمها على هيئة تموجات تُقابل نُقطة الصفر وتقطع محور “X” في كِلا الجانبين السلبي والإيجابي.
- الصيغة الرياضية: y=sin (x) y = cos (x), y = tan (x),
8- الدالة اللوغاريتمية
- من أنواع الدوال التحليلية.
- يكون شكلها تامًّا عند الرسم.
- لا يُمكنها أن تُقابل الصفر نهائيًا.
- يُمكن أن تُشتق الدالة اللوغارتمية إلى عدد لا نهائي من القيّم.
- دائمًا ما تكون ناتج القيّم عقدية.
- الصيغة الرياضية: (f(x)=loga (x
9- الدالة الأسية
- تتمثل شكل الدالة الأسية في ” ax“؛ بحيث يكون الـ ” x” لا يُساوي الواحد الصحيح.
- إذا كانت قيمة “a” أصغر من 1 يُطلق عليها دالة تناقصية.
- في حالة كانت قيمة “a” أكبر من واحد تُعرف بالدالة التزايدية.
- الصيغة الرياضية: f(x)=ax, a > 0, a ≠1
10- الدالة التكعيبية
- يُطلق عليها دالة مُتعددة الحدود من الدرجة الثالثة.
- إذا كانت جميع القيم حقيقة فإن الناتج يكون عددًا حقيقيًا.
- الصيغة الرياضية: f (x) = ax3 + bx2 + cx + d
تغيرات الدوال
- التغير المُركب: إحدى الحالات التي تخضع فيها الدالة إلى التغيران “الطردي والعكسي” في نفس الوقت، وينعكس أثرها على النسبة بين المُتغيرين وقيمتهما.
- التغير الطردي: يظهر تأثيرها على كِلا المُتغيرات في نفس الوقت، فإذا زاد أحدها زاد الآخر في نفس الوقت، فيكون التغير مُتناسبًا.
- التغير العكسي: يظهر أثر الدالة على المُتغيرين، فيكون الناتج من الدالة عكسيًا فإذا زاد أحدهما قل الآخر… والعكس.
ما الفائدة من دراسة الدوال؟
- تُستخدم الدوال في كافة المجالات في الحياة؛ حيث إنها تُخطط للحصول على القيم الدقيقة.
- التعمُق في إيجاد الحلول الفيزيائية للمشاكل المُختلفة.
- المُساعدة على التأقلم والتطور في أساليب العيش.
- التعرف على سلوكيات الظواهر المُختلفة.
- إيجاد القوانين المُبسطة من أجل اختصار الدراسات المُختلفة.
- إيجاد قيم التغيرات؛ مما يُسهم في الوصول إلى طبيعة العلاقة بين المُتغيرات وفهمها.
لا يفوتك أيضًا: يركض مازن 1.5 كيلو متر كل صباح
خاتمة بحث عن الدوال
تُعتبر الدوال هي إحدى العمليات الرياضية الهامّة المسؤولة عن إنتاج قيمة مُهمة؛ والتي يلزم التطبيق عليها جيّدًا، حيث إن أي خطأ حسابي بسيط يؤثر على قيمة الدالة بالكامل.
تحميل بحث عن الدوال PDF
قد تكون الدوال من المسائل الصعبة التي تواجه الطُلاب في بداية دراستها، إلا أنها بسيطة تتطلب بعض التركيز والتطبيق.. لذا احرص على دراستها من البداية جيّدًا حتى لا تواجه صعوبات في الحل.









